Simple Linear Regression Using Regression Procedure

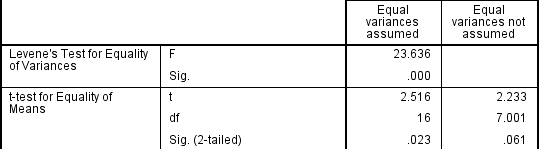
Introduction
Linear regression is the next step up after correlation. Linear regression, also known as simple linear regression or bivariate linear regression, is used when we want to predict the value of a dependent variable based on the value of an independent variable. The variable we want to predict is called the dependent variable (or sometimes, the outcome variable). The variable we are using to predict the other variable's value is called the independent variable (or sometimes, the predictor variable).

 

Types of Regression

A regression models the past relationship between variables to predict their future behavior. As an example, imagine that your company wants to understand how past advertising expenditures have related to sales in order to make future decisions about advertising. The dependent variable in this instance is sales and the independent variable is advertising expenditures.

 

Usually, more than one independent variable influences the dependent variable. You can imagine in the above example that sales are influenced by advertising as well as other factors, such as the number of sales representatives and the commission percentage paid to sales representatives. When one independent variable is used in a regression, it is called a simple regression; when two or more independent variables are used, it is called a multiple regression

 

Regression Models

Regression models can be either linear or nonlinear. A linear model assumes the relationships between variables are straight-line relationships, while a nonlinear model assumes the relationships between variables are represented by curved lines. In business you will often see the relationship between the return of an individual stock and the returns of the market modeled as a linear relationship, while the relationship between the price of an item and the demand for it is often modeled as a nonlinear relationship

 

Scatter Plots

Scatter plots are effective in visually identifying relationships between variables. These relationships can be expressed mathematically in terms of a correlation coefficient, which is commonly referred to as a correlation. Correlations are indices of the strength of the relationship between two variables. They can be any value from –1 to +1.

 

Regression Lines

Characterize the relation between the response variable and the predictor variable. he regression line is the line with the smallest possible set of distances between itself and each data point. As you can see, the regression line touches some data points, but not others. The distances of the data points from the regression line are called error terms.

 

Error Terms

A regression line will always contain error terms because, in reality, independent variables are never perfect predictors of the dependent variables. There are many uncontrollable factors in the business world. The error term exists because a regression model can never include all possible variables; some predictive capacity will always be absent, particularly in simple regression.

 

Least-squares Method

To determine the line that is as close as possible to all the datelines.

The typical procedure for finding the line of best fit is called the least-squares method. Specifically by determining the line that minimizes the sum of the squared vertical distances between the data points and the fitted line. The estimated parameters are beta hat sub zero and beta hat one - These least square estimators are often called BLUE (Best Linear Unbiased Estimators). These estimated parameters should closely approximate the true population parameters - beta sub zero and beta sub one. 

In this calculation, the best fit is found by taking the difference between each data point and the line, squaring each difference, and adding the values together. The least-squares method is based upon the principle that the sum of the squared errors should be made as small as possible so the regression line has the least error.  The process of finding the coefficients of a regression line by minimizing the squared error term.
 

Once this line is determined, it can be extended beyond the historical data to predict future levels of product awareness, given a particular level of advertising expenditure.

Measuring how well a Model Fits a data
How much better is the model that takes the predictor variable to account than a model ignores the predictor variable. To find out you can compare the Simple linear Regression Model to a Baseline Model.

Types of Variability
Explained Variability (SSM) - Is the difference between the regression line and the mean of the response variable
Unexplained (SSE) - Is the difference between the observed values and the regression lines. The error sum of squares is the amount of variability that your model fails to explains.
Total Variability - The total variability is the difference between the observed value and the mean of the response variables.

 

When do we do Simple Linear Regression?

We run simple linear regression when we want to access the relationship between two continuous variables

What SAS procedures do we use to find regression?

The REG procedure is one of many regression procedures in the SAS System. It is a general-purpose procedure for regression, while other SAS regression procedures provide more specialized applications. Other SAS/STAT procedures that perform at least one type of regression analysis are the CATMOD, GENMOD, GLM, LOGISTIC, MIXED, NLIN, ORTHOREG, PROBIT, RSREG, and TRANSREG procedures.

PROC REG provides the following capabilities:

• multiple MODEL statements
• nine model-selection methods
• interactive changes both in the model and the data used to fit the model
• linear equality restrictions on parameters
• tests of linear hypotheses and multivariate hypotheses
• collinearity diagnostics
• correlation or crossproduct input
• predicted values, residuals, studentized residuals, confidence limits, and influence statistics
• requested statistics available for output through output data sets

plots:

• plot model fit summary statistics and diagnostic statistics
• produce normal quantile-quantile (Q-Q) and probability-probability (P-P)
• plots for statistics such as residuals specify special shorthand options to plot ridge traces, confidence intervals, and prediction intervals
• display the fitted model equation, summary statistics, and reference lines on the plot
• control the graphics appearance with PLOT statement options and with global graphics statements including the TITLE, FOOTNOTE, NOTE, SYMBOL, and LEGEND statements
• paint” or highlight line-printer scatter plots
• produce partial regression leverage line-printer plots

In the simplest method, PROC REG fits the complete model that you specify. The other eight methods involve various ways of including or excluding variables from the model. You specify these methods with the SELECTION= option in the MODEL statement.

1. NONE no model selection. This is the default. The complete model specified in the MODEL statement is fit to the data.
2. FORWARD forward selection. This method starts with no variables in the model and adds variables.
3. BACKWARD backward elimination. This method starts with all variables in the model and deletes variables.
4. STEPWISE stepwise regression. This is similar to the FORWARD method except that variables already in the model do not necessarily stay
5. there.
6. MAXR forward selection to fit the best one-variable model, the best two variable model, and so on. Variables are switched so that R2 is maximized.
7. MINR similar to the MAXR method, except that variables are switched so that the increase in R2 from adding a variable to the model is minimized.
8. RSQUARE finds a specified number of models with the highest R2 in a range of model sizes.
9. ADJRSQ finds a specified number of models with the highest adjusted R2 in a range of model sizes.
10. CP finds a specified number of models with the lowest Cp in a range of model sizes.

SIMPLE LINEAR REGRESSION

Simple linear regression is used to predict the value of a dependent variable from the value of an independent variable.

For example, in a study of factory workers you could use simple linear regression to predict a pulmonary measure, forced vital capacity (FVC), from asbestos exposure. That is, you could determine whether increased exposure to asbestos is predictive of diminished FVC. The following SAS PROC REG code produces the simple linear regression equation for this analysis:

PROC REG ;
MODEL FVC=ASB;
RUN ; 

The Simple Linear Regression Model

The regression line that SAS calculates from the data is an estimate of a theoretical line describing the relationship between the independent variable ( X ) and the dependent variable ( Y ).A simple linear regression analysis is used to develop an equation (a linear regression line) for predicting the dependent variable given a value ( x ) of the independent variable. The regression line calculated by SAS is

Y =  a + bx

where a and b are the least - squares estimates of α and β.

The null hypothesis that there is no predictive linear relationship between the two variables is that the slope of the regression equation is zero. Specifically, the hypotheses are:

H 0 : β = 0
H a : β ≠ 0

A low p - value for this test (say, less than 0.05) indicates significant evidence to conclude that the slope of the line is not 0 — that is, knowledge of X would be useful in predicting Y.

 

Suppose that a response variable Y can be predicted by a linear function of a regressor variable X. You can estimate beta sub zero, the intercept, and beta sub 1, the slope, in

 

for the observations i = 1; 2; : : : ; n. Fitting this model with the REG procedure requires only the following MODEL statement, where y is the outcome variable and x is the regressor variable.

 

proc reg;

model y=x;

run;

Notice that the MODEL statement is used to tell SAS which variables to use in the analysis. As in the ANOVA procedure the MODEL statement has the following form:

MODEL dependentvar = independentvar ;

where the dependent variable ( dependentvar ) is the measure you are trying to predict
and the independent variable ( independentvar ) is your predictor.

To fit the Regression models to our data we use the REG procedure, Here is the basic syntax for the Proc Reg procedure to perform a simple linear regression

PROC REG DATA = SAS dataset <options>;
         MODEL dependent (response)  = regressor (predictor) <options>;
RUN ;
QUIT;


Assumptions

1. The mean of Y is linearly related to X
2. Errors are normally distributed with a mean of zero
3. Errors have equal variances
4. Errors are independent
5. Remember the predictor and response variables should be continuous variables

Confidence Intervals and Prediction Intervals
To display Confidence Interval and Prediction Interval you can include the Options CLM and CLI in your Model statement
CLI produces Confidence interval for a Individual Predicted Value
CLM produces a Confidence Interval for a Mean Predicted Value for each Individual Observation
Also add a ID Statement to print the Output Statistics

Output Statistics
The 95% CL Mean are the Intervals for the Mean Y value for a particular X value. The columns labeled 95% CL Predict are the lower and upper prediction limits. These are intervals for future value of Y at a particular value of X.
The Residual is the dependent variable minus the Predicted variable

How does regression work to enable Prediction?
Regression is a way to predict the future relationship between two random variables, given a limited set of historical information. This scatter plot represents the historical relationship between an independent variable, shown on the x-axis, and a dependent variable, shown on the y-axis.
The line that best fits the available data is the one with the smallest possible set of distances between itself and each data point. To find the line with the best fit, calculate the actual distance between each data point and every possible line through the data points.
The line with the smallest set of distances between the data points is the regression line. The trajectory of this line will best predict the future relationship between the two variables.
The concept of predictability is an important one in business. Common business uses for linear regression include forecasting sales and estimating future investment returns

Here is an Example in SAS: Initially when I saw this example I thought what is this! Then I realized  this is  a really a wonderful example.

EXAMPLE SIMPLE LINEAR REGERSSION IN SAS

A random sample of fourteen elementary school students is selected from a school, and each student is measured on a creativity score ( X ) using a new testing instrument and on a task score ( Y ) using a standard instrument. The task score is the mean time taken to perform several hand – eye coordination tasks. Because administering the creativity test is much cheaper, the researcher wants to know if the CREATE score is a good substitute for the more expensive TASK score. The data are shown below in the following SAS code that creates a SAS data set named ART with variables SUBJECT, CREATE and TASK. Note that the SUBJECT variable is of character type so the name is followed by a dollar sign ($).

 

DATA ART;

INPUT SUBJECT $ CREATE TASK;

DATALINES;

AE 28 4.5

FR 35 3.9

HT 37 3.9

IO 50 6.1

DP 69 4.3

YR 84 8.8

QD 40 2.1

SW 65 5.5

DF 29 5.7

ER 42 3.0

RR 51 7.1

TG 45 7.3

EF 31 3.3

TJ 40 5.2

;

RUN;

The SAS code necessary to perform the simple linear regression analysis for this data is

ODS HTML;
ODS GRAPHICS ON;
PROC REG DATA=ART;
MODEL TASK=CREATE / CLM CLI;
TITLE “Example simple linear regression using PROC REG”;
RUN ;
ODS GRAPHICS OFF;
ODS HTML CLOSE;
QUIT;

 

If you are running SAS 9.3 or later, you can leave off the ODS statements.

 

“Example simple linear regression using PROC REG”

The REG Procedure

Model: MODEL1

Dependent Variable: TASK

 

Number of Observations

Number of Observations Read	14
Number of Observations Used	14

Analysis of Variance

Analysis of Variance
Source	DF	Sum of Squares	Mean Square	F Value	Pr > F
Model	1	13.70112	13.70112	5.33	0.0396
Error	12	30.85388	2.57116
Corrected Total	13	44.55500

Fit Statistic

Root MSE	1.60348	R-Square	0.3075
Dependent Mean	5.05000	Adj R-Sq	0.2498
Coeff Var	31.75213

Parameter Estimates

Parameter Estimates
Variable	DF	Parameter Estimate	Standard Error	t Value	Pr > |t|
Intercept	1	2.16452	1.32141	1.64	0.1273
CREATE	1	0.06253	0.02709	2.31	0.0396

 

  

 

 

 

Note that because you want to predict TASK from CREATE the MODEL statement is

MODEL TASK=CREATE;

Where TASK is the dependent (predicted) variable and CREATE is the independent (predictor) variable. The (partial) output from this analysis is shown next:

The Analysis of Variance table provides an overall test of the model. This test is duplicated in the Parameters table and is not shown here.

Root MSE	1.60348	R-Square	0.3075
Dependent Mean	5.05000	Adj R-Sq	0.2498
Coeff Var	31.75213

 

The R-Square table provides you with measures that indicate the model fit. The most commonly referenced value is R-Square which ranges from 0 to 1 and indicates the proportion of variance explained in the model. The closer R-Square is to 1, the better the model fit. According to Cohen (1988), an R-Square of 0.31 indicates a large effect size, which is an indication that CREATE is predictive of TASK.

Parameter Estimates
Variable	DF	Parameter Estimate	Standard Error	t Value	Pr > |t|
Intercept	1	2.16452	1.32141	1.64	0.1273
CREATE	1	0.06253	0.02709	2.31	0.0396

 

The Parameter Estimate table provides the coefficients for the regression equation, and a test of the null hypothesis that the slope is zero. (p=0.0396 indicates that you would reject the hull hypothesis and conclude that the slope is not zero.)

In this example, the predictive equation (using the estimates in the above table) is

TASK = 2.126452 + CREATE * 0.06253

Thus, if you have a value for CREATE, you can put that value into the equation and predict TASK.
 

The question is, how good is the prediction? 
Several plots are provided to help you evaluate the regression model. The following graph shows the predictive line and a confidence bands around that line. When the bands are tight around the line, it indicates better prediction, and a large band around the line indicates a less accurate prediction. In this case the confidence bands (particularly the prediction band) are fairly wide. This indicates that although CREATE is predictive of TASK, there prediction is only moderately accurate. When the R-Square is much higher, say over 0.70, the band will be tighter, and predictions will be more accurate.   

 

Reference: Jacob Cohen (1988). Statistical Power Analysis for the Behavioral Sciences (second ed.). Lawrence Erlbaum Associates.

Reading the Result

First look at the number of data Read and the number of data Used. If its the same it indicates that SAS detects no missing values for the variables.

Next the Analysis of variance table displays the  Overall Fit for the Model. variability explained in the reponse and the variability explained by the regression line. The Source column indicates the source of variability. Model is the between group variability that your model explains (SSM). Error is the within group variability that your Model does not explain (SSE). Corrected total is the total variability in the response.

The DF column indicates the Degrees of Freedom association with each source of variability, which are independent pieces of information for each source The Model DF is 1 because the Model has one continuous predictor term. So we are estimating one parameter beta sub1. The Corrected Total DF
n-1 which is 14 - 1 = 13. The Error DF is what is left over; it is the difference between the Total DF and the Model DF 13-1 = 12. You can think of Degrees of freedom as the number of independent pieces of information.

The Sum of Squares indicates the Amount of Variability associated with each source of variability.

Mean Square column indicated the Ratio of Model Sum of Squares divided by DF which gives us the average sum of squares of the Model.
The Mean Square Error is the variance of the population. This is calculated by the Error sum of squares by the Error DF which gives the Average Sum of Squares.
The F value is the ratio of the Mean square of the Model divided by the Mean Square for the Error. This ratio explains the variability that the regression line explains to the variability of the regression line that doesn't explain. The p-value is less than
If the p value is less the .05 and we reject the NULL Hypotheses. If the Null hypotheses is true it means the Model with CREATE is not any better than the base. However in this case the Model fit the data better than the baseline model

The third part of the displays Summary Fit measures for the Model
Root MSE - is the Square root of the Mean Square Error in the ANOVA table
Dependent Mean - Average of Response variable for all candidates
Coeff Var - Size of the Standard Deviation relative to the mean
R Square - Calculated by diving the Mean Square of the Model by the total Sum of Square. The R square value is between Zero and 1. Measures the proportion of variance observed in response that the regression line explains

What percentage of variation in the response variable does the model explain? Approximately 30%
Adjusted R Square - This is useful in Multiple Regression

The Parameter Estimates table defines the Model for the data. This provides separate estimates and Significance tests for each Model Parameter.  Gives the parameter estimate for the Intercept as
2.16452 (The estimated value of TASK when CREATE is equal to zero) and the predictor variable parameter estimate as 0.06253. If the TASK increase by one unit the CREATE increase by 0.06253 units. We are interested at looking at the relationship between the TAST and CREATE. The p value is to explain the variability of response variable. Since only one predictor variable is used it is equal to the p-value of the overall test. Because the p-value 0.0396 is less than .05 there is significance in variability of TASK

Finally lets enter the results in the equation of Simple Linear Regression
Response variable = Intercept variable + Slope parameter x Predictor variable
TASK = 2.16452 + 0.06253 * CREATE (This is the estimated Regression Equation)

The Graphical Part of the Output
If you have a look at the Fit Plot the shaded area refers to the Confidence interval around the Mean. A confidence. A 95% Confidence Interval gives a range of values which is likely to include an Unknown Population parameter. This indicates that we are 95% confident our interval contains true population mean Y for a particular X. The wider the confidence interval the less precise.

The dashed lines indicate the prediction interval of the individual Observations. This means that you are 95% confident that your interval contains the new observation.

Note that by default Proc Reg displays the Model Statistics in the Plot

How do I store the results in a new dataset instead of printing it?
Use the Proc Reg to write the parameter estimates to Output dataset instead of producing the usual results and graphs. You can then use two options to the Proc Reg statement
- The NOPRINT option suppresses the normal display of regression results
- the OUTEST option creates a output dataset containing Parameter Estimates and other summary statistics from the regression model

References:

http://www0.gsb.columbia.edu/premba/analytical/s7/s7_6.cfm

http://www.stattutorials.com/SAS/TUTORIAL-PROC-REG-SIMPLE-REGRESSION.htm 

Independent t-Test for Two Sample

Introduction
The independent t-test, also called the two sample t-test or student's t-test, is an inferential statistical test that determines whether there is a statistically significant difference between the means in two unrelated groups.

The independent-samples t-test (or independent t-test, for short) compares the means between two unrelated groups on the same continuous, dependent variable. For example, you could use an independent t-test to understand whether first year graduate salaries differed based on gender (i.e., your dependent variable would be "first year graduate salaries" and your independent variable would be "gender", which has two groups: "male" and "female"). Alternately, you could use an independent t-test to understand whether there is a difference in test anxiety based on educational level (i.e., your dependent variable would be "test anxiety" and your independent variable would be "educational level", which has two groups: "undergraduates" and "postgraduates").

Hypothesis for the Independent t-Test
The null hypothesis for the independent t-test is that the population means from the two unrelated groups are equal:
H₀: u₁ = u₂ (Means of two groups are equal) 
In most cases, we are looking to see if we can show that we can reject the null hypothesis and accept the alternative hypothesis, which is that the population means are not equal:
H_A: u₁ ≠ u₂ (Means of two groups are not equal) 
To do this, we need to set a significance level (alpha) that allows us to either reject or accept the alternative hypothesis. Most commonly, this value is set at 0.05.

What do we need to run an independent Test?
In order to run an independent t-test, you need the following:

• One independent, categorical variable that has two levels (An independent variable, sometimes called an experimental or predictor variable, is a variable that is being manipulated in an experiment in order to observe the effect on a dependent variable, sometimes called an outcome variable)
• One dependent variable.

Unrelated Groups
Unrelated groups, also called unpaired groups or independent groups, are groups in which the cases in each group are different. Often we are investigating differences in individuals, which means that when comparing two groups, an individual in one group cannot also be a member of the other group and vice versa. An example would be gender - an individual would have to be classified as either male or female - not both.

Assumptions
When you choose to analyze your data using an independent t-test, part of the process involves checking to make sure that the data you want to analyze can actually be analyzed using an independent t-test. You need to do this because it is only appropriate to use an independent t-test if your data "passes" six assumptions that are required for an independent t-test to give you a valid result.
Do not be surprised if, when analyzing your own data, one or more of these assumptions is violated (i.e., is not met). This is not uncommon when working with real-world data rather than textbook examples, which often only show you how to carry out an independent t-test when everything goes well! However, don't worry. Even when your data fails certain assumptions, there is often a solution to overcome this. First, let's take a look at these six assumptions:

• Assumption #1: The independent t-test requires that the dependent variable is approximately normally distributed within each group. We can test for this using a multitude of tests, but the Shapiro-Wilks Test or a graphical method, such as a Q-Q Plot, are very common. Your dependent variable should be measured on a continuous scale (i.e., it is measured at the interval or ratio level). Examples of variables that meet this criterion include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100), weight (measured in kg), and so forth.  
• Assumption #2: Your independent variable should consist of two categorical, independent groups. Example independent variables that meet this criterion include gender (2 groups: male or female), employment status (2 groups: employed or unemployed), smoker (2 groups: yes or no), and so forth.
• Assumption #3: You should have independence of observations, which means that there is no relationship between the observations in each group or between the groups themselves. For example, there must be different participants in each group with no participant being in more than one group. This is more of a study design issue than something you can test for, but it is an important assumption of the independent t-test. If your study fails this assumption, you will need to use another statistical test instead of the independent t-test (e.g., a paired-samples t-test).  
• Assumption #4: There should be no significant outliers. Outliers are simply single data points within your data that do not follow the usual pattern (e.g., in a study of 100 students' IQ scores, where the mean score was 108 with only a small variation between students, one student had a score of 156, which is very unusual, and may even put her in the top 1% of IQ scores globally). The problem with outliers is that they can have a negative effect on the independent t-test, reducing the validity of your results. 
• Assumption #5: Your dependent variable should be approximately normally distributed for each group of the independent variable. We talk about the independent t-test only requiring approximately normal data because it is quite "robust" to violations of normality, meaning that this assumption can be a little violated and still provide valid results.  
• Assumption #6: There needs to be homogeneity of variances. You can test this assumption using Levene’s test for homogeneity of variances. The independent t-test assumes the variances of the two groups you are measuring to be equal. If your variances are unequal, this can affect the Type I error rate. The assumption of homogeneity of variance can be tested using Levene's Test of Equality of Variances. If you have run Levene's Test of Equality of Variances, you will get a result similar to that below:
  
  
  This test for homogeneity of variance provides an F statistic and a significance value (p-value). We are primarily concerned with the significance level - if it is greater than 0.05, our group variances can be treated as equal. However, if p < 0.05, we have unequal variances and we have violated the assumption of homogeneity of variance.

What to do when you violate the Normal Assumptions
If you find that either one or both of your group's data is not approximately normally distributed and groups sizes differ greatly, you have two options:
(1) transform your data so that the data becomes normally distributed or
(2) run the Mann-Whitney U Test which is a non-parametric test that does not require the assumption of normality

Overcoming the violation of Homogeneity of Variance
If the Levene's Test for Equality of Variances is statistically significant, and therefore indicates unequal variances, we can correct for this violation by not using the pooled estimate for the error term for the t-statistic, and also making adjustments to the degrees of freedom using the Welch-Satterthwaite method. However, you can see the evidence of these tests as below:

 

From the result of Levene's Test for Equality of Variances, we can reject the null hypothesis that there is no difference in the variances between the groups and accept the alternative hypothesis that there is a significant difference in the variances between groups. The effect of not being able to assume equal variances is evident in the final column of the above figure where we see a reduction in the value of the t-statistic and a large reduction in the degrees of freedom (df). This has the effect of increasing the p-value above the critical significance level of 0.05. In this case, we therefore do not accept the alternative hypothesis and accept that there are no statistically significant differences between means. This would not have been our conclusion had we not tested for homogeneity of variances.

How to use an Independent T-Test
This level assumes that you will use a software package to perform a t-test. If you want to know how to do it by hand, read level two. The result of using a t-test is that you know how likely it is that the difference between your sample means is due to sampling error. This is presented as a probability and is called a p-value. The p-value tells you the probability of seeing the difference you found (or larger) in two random samples if there is really no difference in the population.Generally, if this p-value is below 0.05 (5%), you can reject the null hypothesis and conclude that there is a statistically significant difference between the two population means. If you want to be particularly strict, you can decide that the p-value should be below 0.01 (1%). The level of p that you choose is called the significance level of the test. The p-value is calculated by first using the t-test formula to produce a t-value. This t-value is then converted to a probability either by software or by looking it up in a t-table. The next topic covers this part of the process

Calculating T Now we will look at the formula for calculating the t-value from an independent t-test. There are two versions of the formula, one for use when the two samples you wish to compare are of equal size, and one for differently sized samples. We will look at the first version because your data is equal in size for each sample and because it is the simpler formula. The unequal sized samples formula is shown in the extra topic section for your information.
The formula is the ratio of the difference between the two sample means to the variation within the two samples. The ratio has the following consequences:

• When the difference between the sample means is large and the variation within each sample is small, t is large;
• When the difference between the sample means is small and the variation within each sample is large, t is small.

In other words, if there is a lot of variation in the values of each sample, it is natural to assume that there will be variation between two samples. In such cases, the t-value will be low.

Here is the formula to calculate the t value for equal sized Independent Samples

It reads: sample mean 1 minus sample mean 2 divided by the square root of (sample variance 1 plus sample variance 2, over n)

• x₁ is read as x1-bar and is the mean of the first sample;
• x₂ is read as x2-bar and is the mean of the second sample;
• The variance is the standard deviation squared (hence s²).
• The subscript numbers (1 and 2 to the bottom right of the x and s in the formula) refer to sample 1 and sample 2;

Reporting the result of a Independent t-Test
When reporting the result of an independent t-test, you need to include the t-statistic value, the degrees of freedom (df) and the significance value of the test (p-value). The format of the test result is: t(df) = t-statistic, p = significance value. Therefore, for the example above, you could report the result as t(7.001) = 2.233, p = 0.061.

For example
Inspection of Q-Q Plots revealed that cholesterol concentration was normally distributed for both groups and that there was homogeneity of variance as assessed by Levene's Test for Equality of Variances. Therefore, an independent t-test was run on the data as well as 95% confidence intervals (CI) for the mean difference. It was found that after the two interventions, It was found that after the two interventions, cholesterol concentrations in the dietary group exercise group (5.80 ± 0.38 mmol/L) (t(38) = 2.470, p = 0.018) with a difference of 0.35 (95% CI, 0.06 to 0.64) mmol/L.

Here is an example of Independent t-Test and how we perform with SAS

When data are collected on subjects where subjects are (hopefully randomly) divided into two groups, this is called an independent or parallel study.  That is, the subjects in one group (treatment, etc) are different from the subjects in the other group.
 

The SAS PROC TTEST procedure
This procedure is used to test for the equality of means for a two-sample (independent group) t-test. For example, you might want to compare males and females regarding their reaction to a certain drug, or one group who receives a treatment compared to another that receives a placebo. The purpose of the two-sample t-test, is to determine whether your data provide you with enough evidence to conclude that there is a difference in mean reaction levels between the two group. In general, for a two-sample t-test you obtain independent random samples of size N1 and N2 and from the two populations of interest, and then you compare the observed sample means.

The typical hypotheses for a two-sample t-test are

H_o: m₁ = m₂           (means of the two groups are equal)
H_a: m₁¹ m₂         (means are not equal)

Key assumptions underlying the two-sample t-test are that the random samples are independent and that the populations are normally distributed with equal variances. (If the data are non-normal, then nonparametric tests such as the Mann-Whitney U are appropriate.)

SAS Syntax:

Simplified syntax for the TTEST procedure is

PROC TTEST <options>;
CLASS variable; <statements>;
RUN;

Common OPTIONS:

• DATA = datasetname: Specifies what data set to use.
• COCHRAN: Specifies that the Cochran and Cox probability approximation is to be used for unequal variances.

Common STATEMENTS:

• CLASS statement: The CLASS statement is required, and it specifies the grouping variable for the analysis.

The data for this grouping variable must contain two and only two values. An example PROC TTEST command is

PROC TTEST DATA=MYDATA;
CLASS GROUP;
VAR SCORE;
RUN;

In this example, GROUP contains two values, say 1 or 2. A t-test will be performed on the variable SCORE.

• VAR variable list;: Specifies which variables will be used in the analysis.
• BY variable list;: (optional) Causes t-tests to be run separately for groups specified by the BY statement.

EXAMPLE:

A biologist experimenting with plant growth designs an experiment in which 15 seeds are randomly assigned to one of two fertilizers and the height of the resulting plant is measured after two weeks. She wants to know if one of the fertilizers provides more vertical growth than the other.

STEP 1. Define the data to be used. (If your data is already in a data set, you don't have to do this step). For this example, here is the SAS code to create the data set for this experiment:

DATA FERT;
INPUT BRAND $ HEIGHT;
DATALINES;
A 20.00
A 23.00
A 32.00
A 24.00
A 25.00
A 28.00
A 27.50
B 25.00
B 46.00
B 56.00
B 45.00
B 46.00
B 51.00
B 34.00
B 47.50
;
RUN;

STEP 2. The following SAS code specifies a two-sample t-test using the FERT dataset.(NOTE: For SAS 9.3, you don't need the ODS statements.)

ODS HTML;
ODS GRAPHICS ON;
PROC TTEST DATA=FERT;
CLASS BRAND;
VAR HEIGHT;
Title 'Independent Group t-Test Example';
RUN;
ODS GRAPHICS OFF;
ODS HTML CLOSE;
QUIT;
 

The CLASS statement specifies the grouping variables with 2 categories (in this case A and B).

The VAR statement specifies which variable is the observed (outcome or dependent) variable.

Interpret the output. The (abbreviated) output contains the following information

BRAND	N	Mean	Std Dev	Std Err	Minimum	Maximum
A	7	25.6429	3.9021	1.4748	20.0000	32.0000
B	8	43.8125	9.8196	3.4717	25.0000	56.0000
Diff (1-2)		-18.1696	7.6778	3.9736

This first table provides means, sd, min and max for each group and the mean difference.

BRAND	Method	Mean	95% CL Mean		Std Dev	95% CL Std Dev
A		25.6429	22.0340	29.2517	3.9021	2.5145	8.5926
B		43.8125	35.6031	52.0219	9.8196	6.4925	19.9855
Diff (1-2)	Pooled	-18.1696	-26.7541	-9.5852	7.6778	5.5660	12.3692
Diff (1-2)	Satterthwaite	-18.1696	-26.6479	-9.6914

    

The next table provides 95% Confidence Limits on both the means and Standard Deviations, and the mean difference using both the pooled (assume variances are equal) and Satterthwaite (assume variances are not equal) methods.

Before deciding which version of the t-test is appropriate, look at this table

Equality of Variances
Method	Num DF	Den DF	F Value	Pr > F
Folded F	7	6	6.33	0.0388

This table helps you determine if the variances for the two groups are equal. If the p-value (Pr>F) is less than 0.05, you should assume UNEQUAL VARIANCES. In this case, the variances appear to be unequal.
   

Therefore... in the t-test table below (for this case) choose the Satterthwaite t-test, and report a p-value of p=0.0008. If the variances were assumed equal, you would report the Pooled variances t-test.

Method	Variances	DF	t Value	Pr > |t|
Pooled	Equal	13	-4.57	0.0005
Satterthwaite	Unequal	9.3974	-4.82	0.0008

Since p<.05, you can conclude that the mean for group B (43.8125) is statistically larger than the mean for group A (25.6429). More formally, you reject the null hypothesis that the means are equal and show evidence that they are different.
 

When you use the ODS GRAPHICS ON option, you get the following graph:

This graph provides a visual comparison of the means (and distributions) of the two groups. In this graph you can see that the mean of group B is larger than the mean of group A. You can also see why the test for equality of variances found that they were not the same (the variance for group A is smaller.)

A complete report of our result
In order to provide enough information for readers to fully understand the results when you have run an independent t-test, you should include the result of normality tests, Levene's Equality of Variances test, the two group means and standard deviations, the actual t-test result and the direction of the difference (if any). In addition, you might also wish to include the difference between the groups along with the 95% confidence intervals.

References

http://www.stattutorials.com/SAS/TUTORIAL-PROC-TTEST-2.htm

http://www.stattutorials.com/SAS/TUTORIAL-PROC-TTEST-INDEPENDENT.htm

Dependent t-Test for Paired Samples

What does this test do?

The dependent t-test (also called paired t-test or paired-samples t-test) compares the mean of two related groups to detect whether there are any statistically significant differences between these means.

What variables do we need for Dependent t-Test?
We need one dependent variable that is measured in an interval or ratio scale. We also need one categorical variable that has only two related groups.

Dependent Samples: When data are collected twice on the same subjects (or matched subjects) the proper analysis is a paired t-test (also called a dependent samples t-test). In this case, subjects may be measured in a before – after fashion, or in a design where a treatment is administered for a time, there is a washout period, and another treatment is administered (in random order for each subject). Or, data might be measured on the same individual in two areas such as one treatment in one eye and another treatment for another eye (or leg, or arm, etc). In these cases the measurement of interest is the difference between the first and second measure. Thus, the null hypothesis (two-sided) is:

H_o: m_difference = 0         (The average difference is 0)

H_a: m_difference ≠ 0         (The average difference is not 0)

What is meant by "related groups"?
A dependent t-test is an example of a "within-subjects" or "repeated-measures" statistical test. This indicates that the same subjects are tested more than once. Thus, in the dependent t-test, "related groups" indicates that the same subjects are present in both groups. The reason that it is possible to have the same subjects in each group is because each subject has been measured on two occasions on the same dependent variable.
For example, you might have measured 10 individuals' (subjects') performance in a spelling test (the dependent variable) before and after they underwent a new form of computerized teaching method to improve spelling. You would like to know if the computer training improved their spelling performance. Here, we can use a dependent t-test because we have two related groups. The first related group consists of the subjects at the beginning (prior to) the computerized spell training and the second related group consists of the same subjects, but now at the end of the computerized training

Does the dependent t-test test for "Changes" or "Differences" between related groups?
The dependent t-test can be used to test either a "change" or a "difference" in means between two related groups, but not both at the same time. Whether you are measuring a "change" or "difference" between the means of the two related groups depends on your study design. The two types of study design are indicated in the following diagrams.

How do you detect differences between experimental conditions using the dependent t-test?
The dependent t-test can look for "differences" between means when subjects are measured on the same dependent variable under two different conditions. For example, you might have tested subjects' eyesight (dependent variable) when wearing two different types of spectacle (independent variable). See the diagram below for a general schematic of this design approach



How do you detect changes in time using the dependent t-test?
The dependent t-test can also look for "changes" between means when the subjects are measured on the same dependent variable, but at two time points. A common use of this is in a pre-post study design. In this type of experiment, we measure subjects at the beginning and at the end of some intervention (e.g., an exercise-training programme or business-skills course). A general schematic is provided below

How do you detect differences between experimental conditions using the dependent t-test?
You can also use the dependent t-test to study more complex study designs although it is not normally recommended. The most common, more complex study design where you might use the dependent t-test is where you have a crossover design with two different interventions that are both performed by the same subjects. One example of this design is where you have one of the interventions act as a control. For example, you might want to investigate whether a course of diet counselling can help people lose weight. To study this you could simply measure subjects' weight before and after the diet counselling course for any changes in weight using a dependent t-test. However, to improve the study design you also include want to include a control trial. During this control trial, the subjects could either receive "normal" counselling or do nothing at all, or something else you deem appropriate. In order to assess this study using a dependent t-test, you would use the same subjects for the control trial as the diet counselling trial. You then measure the differences between the interventions at the end, and only at the end, of the two interventions. Remember, however, that this is unlikely to be the preferred statistical analysis for this study design.

What are the assumptions of the dependent t-test?

• The types of variables
• The distribution of the differences between the scores of the two related groups needs to be normally distributed - We do this by simply subtracting each individuals' score in one group from their score in the other related group and then testing for normality in the normal way  It is important to note that the two related groups do not need to be normally distributed themselves - just the differences between the groups.

What hypothesis is being tested?
The dependent t-test is testing the null hypothesis that there are no differences between the means of the two related groups. If we get a significant result, we can reject the null hypothesis that there are no significant differences between the means and accept the alternative hypothesis that there are statistically significant differences between the means. We can express this as follows:

H₀: µ₁ = µ₂

H_A: µ₁ ≠ µ₂

What is the advantage of dependent t-test over independent t-test?
Before we answer this question, we need to point out that you cannot choose one test over the other unless your study design allows it. What we are discussing here is whether it is advantageous to design a study that uses one set of subjects whom are measured twice or two separate groups of subjects measured once each. The major advantage of choosing a repeated-measures design (and therefore, running a dependent t-test) is that you get to eliminate the individual differences that occur between subjects - the concept that no two people are the same - and this increases the power of the test. What this means is that if you are more likely to detect any significant differences, if they do exist, using the dependent t-test versus the independent t-test.

Can the dependent t-test used to compare different subjects?
Yes, but this does not happen very often. You can use the dependent t-test instead of using the usual independent t-test when each subject in one of the independent groups is closely related to another subject in the other group on many individual characteristics. This approach is called a "matched-pairs" design. The reason we might want to do this is that the major advantage of running a within-subject (repeated-measures) design is that you get to eliminate between-groups variation from the equation (each individual is unique and will react slightly differently than someone else), thereby increasing the power of the test. Hence, the reason why we use the same subjects - we expect them to react in the same way as they are, after all, the same person. The most obvious case of when a "matched-pairs" design might be implemented is when using identical twins. Effectively you are choosing parameters to match your subjects on which you believe will result in each pair of subjects reacting in a similar way.

Here is the formula for a paired t-test.



The top of the formula is the sum of the differences (i.e. the sum of d). The bottom of the formula reads as:
The square root of the following: n times the sum of the differences squared minus the sum of the squared differences, all over n-1.

• The sum of the squared differences: ∑d² means take each difference in turn, square it, and add up all those squared numbers.
• The sum of the differences squared: (∑d)²means add up all the differences and square the result.

Brackets around something in a formula mean (do this first), so (∑d)² means add up all the differences first, then square the result.

How do I report the result of a dependent t-test?
You need to report the test as follows:

where df is N - 1, where N = number of subjects


Here is a example of Paired t-Test

Consider the data from a paper by Raskin and Unger (1978) where four diabetic patients were used to compare the effects of insulin infusion regimens. One treatment was insulin and somatostatin (IS) and the other treatment was insulin, somatostatin and gulcagon (ISG). Each subject was given each treatment with a period of washout between treatments. The data follow:

Patient	Treatment
Number	IS	ISG	Difference
1	14	17	3
2	6	8	2
3	7	11	4
4	6	9	3
Mean	8.25	11.25	3.0
S.E.M.	1.9	2	.40

 

A paper by Thomas Louis (1984) looked at this data using both types of t-tests (Dependent and Independent t-Test). The correct version of the t-test to use for this data set is the paired t-test since each patient is observed twice

 

Paired t-test analysis: The calculations for this test can be performed using the following SAS code:
 

data diabetic;

input IS ISG;

datalines;

14     17

6      8

7      11

6      9

 

ODS HTML;

PROC TTEST;

  PAIRED IS*ISG;

RUN;

ODS HTML CLOSE;

 

The (partial) output is as follows. Note that the analysis is performed on the mean of the differences (-4.299) and that the standard error of the difference is 0.41

 

Difference	N	Lower CL Mean	Mean	Upper CL Mean	Lower CL Std Dev	Std Dev	Upper CL Std Dev	Std Err
IS - ISG	4	-4.299	-3	-1.701	0.4625	0.8165	3.0443	0.4082

 

The paired t-test yields p=0.005, which is statistically significant.  

T-Tests
Difference	DF	t Value	Pr > |t|
IS - ISG	3	-7.35	0.0052

 

The reason that the paired t-test found significance when the independent t-test on the same data did not achieve significance is because the paired analysis is the more correct analysis and therefore it is able to make use of a much smaller standard error (of the mean difference rather than pooled.)

In his paper, Louis explains that to achieve the power of this paired t-test, an independent group t-test (parallel test) would require 14 times as many subjects. Thus, when the model is appropriate, the paired t-test can be a more powerful design to analysis your data. On the other hand, if you use a paired analysis on independent group data you will get incorrect and misleading results. Therefore, carefully consider how your experiment is designed before you select which t-test to perform.

 

References:

 

https://statistics.laerd.com/statistical-guides/dependent-t-test-statistical-guide.php

http://www.stattutorials.com/SAS/TUTORIAL-PROC-TTEST-2.htm